Las características de Matemáticas

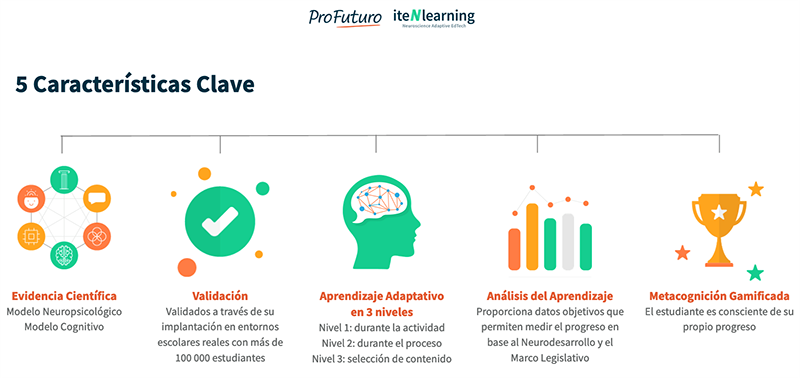
¿Cuáles son sus características fundamentales? Aunque ya las hemos avanzado al hablar de los instrumentos educativos profesionales, a continuación nos detendremos en cómo estas características generales se aplican concretamente a Matemáticas

Las evidencias científicas

Matemáticas se basa en tres tipos de evidencias: evidencias científicas, evidencias empíricas y evidencias de aprendizaje.

• Las evidencias científicas: las experiencias de aprendizaje que Matemáticas proporciona a los estudiantes son las mejores para su neurodesarrollo, al estar basadas en el modelo neuropsicológico y el modelo cognitivo que establecen cómo se alcanza un neurodesarrollo competencial óptimo.

• Las evidencias empíricas: Matemáticas incorpora multitud de acciones educativas con tamaños de efecto óptimos (los tamaños de efecto son índices que miden la magnitud de un efecto de tratamiento). Es decir, incorpora todas aquellas acciones que han probado ser más efectivas para el aprendizaje de las Matemáticas. Por ejemplo, entre otras muchas, el establecimiento de los objetivos de aprendizaje (en cada ejercicio muestra cuáles son los objetivos de aprendizaje y su correlación con el currículo), la enseñanza explícita (siempre hay un ejemplo de ejercicio explicado, secuenciado y práctico, con instrucciones) o la autoevaluación (después de cada sesión se incluyen preguntas para que el estudiante autoevalúe su actuación).

• Las evidencias de aprendizaje: Matemáticas cuenta con sistemas de análisis de aprendizaje que permiten recoger y analizar datos, en tiempo real, acerca del estado de neurodesarrollo de un estudiante y/o grupo de estudiantes. Así proporciona a docentes datos objetivos que le permitan tomar las mejores decisiones de cara a generar mejoras en los procesos de enseñanza y aprendizaje de sus alumnos

La validación

La segunda característica de Matemáticas es la validación. Los instrumentos educativos profesionales tienen que haber sido validados en tres niveles: una validación por juicio de expertos, es decir, especialistas que conocen bien el modelo cognitivo y el modelo neuropsicológico, deben asegurar que el proceso de convergencia entre ciencia y tecnología se ha desarrollado correctamente. En segundo lugar tiene que haber unos estudios estadísticos que verifiquen que el instrumento responde bien cuando se aplican en distintos entornos educativos. Y por último, tiene que haber estudios de caso que demuestren que han conseguido esta mejora en los estudiantes. Matemáticas ha sido validado a través de su implantación en entornos escolares reales con más de 100.000 estudiantes.

Aprendizaje adaptativo en tres niveles

Los instrumentos educativos profesionales tienen que tener tres niveles de aprendizaje adaptativo, distintos y complementarios, en función de las necesidades del estudiante, para que las experiencias de aprendizaje que proporcione sean positivas para esa persona. Estos niveles trabajan de forma coordinada y simultánea, potenciándose entre sí, y son los siguientes:

• Nivel 1: tratamiento del error. Se produce a partir de la interacción entre el estudiante y el instrumento, en este caso Matemáticas, que se adapta a las actividades del alumno en función de los resultados de su trabajo, proporcionándole información sobre sus puntos de dificultad, así como información conceptual que puede mejorar la comprensión del estudiante.

• Nivel 2: curvas de memoria y aprendizaje. El sistema de Matemáticas se adapta al ritmo de desarrollo de cada estudiante adecuando y creando sus sesiones de trabajo para convertirlas en diferentes oportunidades de aprendizaje (por ejemplo, aquellas que se presentan por primera vez, aquellas que ya se han presentado pero están en proceso de construcción, aquellas que han sido adquiridas pero no consolidadas…).

• Nivel 3: selección inteligente de contenidos. Matemáticas genera las oportunidades de aprendizaje (contenidos) adecuados para el estudiante en cada momento, optimizando así el proceso de enseñanza y aprendizaje en función de sus necesidades y del currículo.

Metacognición gamificada

Matemáticas permite que el estudiante se haga consciente de su propio proceso de neurodesarrollo y le enseña a pensar sobre su propio aprendizaje, lo que le permitirá tomar control de su propio proceso de aprendizaje y desarrollar su competencia de aprender a aprender.

Análisis del aprendizaje

Matemáticas proporciona información clara y detallada sobre los procesos de neurodesarrollo y desempeño de los estudiantes en tiempo real, facilitando al docente datos objetivos que le permitan tomar las mejores decisiones en lo que se refiere al aprendizaje de sus estudiantes.